
(简答题)
设二维正态随机变量,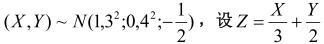 试求: (1)Z的数学期望和方差; (2)ρxz; (3)判断X与与Z的独立性。
试求: (1)Z的数学期望和方差; (2)ρxz; (3)判断X与与Z的独立性。
正确答案

答案解析
略
相似试题
(简答题)
设二维正态随机变量,试求: Z的数学期望和方差; ρxz; 判断X与Z的独立性。
(简答题)
设随机变量X与Y的概率分布分别如下表所示。 (1)求二维随机变量(X,Y)的概率分布; (2)求Z=XY的概率分布。
(简答题)
设随机变量X,Y,Z相互独立,且E(X)=5,E(Y)=11,E(Z)=8,求下列随机变量的数学期望. (1)U=2X+3Y+1; (2)V=YZ-4X.
(简答题)
设二维随机变量(X,Y)的联合概率密度为 试求:(1); (2)联合分布函数F(x,y)
(简答题)
设二维随机变量(X,Y)的联合概率密度为 试求: (1)P{0≦X≦1,0≦Y≦2}; (2)联合分布函数F{x,y}
(简答题)
设二维随机变量(X,Y)服从二维正态分布求(X,Y)的联合概率密度。
(简答题)
设二维连续型随机变量(X,Y)的联合密度函数为 试求: (1)相关系数; (2)X与Y是否相互独立?是否不相关?
(简答题)
设二维随机变量(X,Y)在区域D={(x,y)|x≥0,y≥0,x+y≤1}上服从均匀分布.求Z=X+Y的分布函数与概率密度.
(简答题)
设二维随机变量(X,Y)的联合概率密度为 求随机变量Z=X+2Y的分布函数和概率密度。


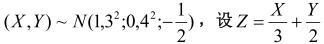 试求: (1)Z的数学期望和方差; (2)ρxz; (3)判断X与与Z的独立性。
试求: (1)Z的数学期望和方差; (2)ρxz; (3)判断X与与Z的独立性。 