
(简答题)
一个四元对称信源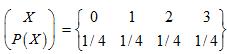 ,接收符号Y={0,1,2,3},其失真矩阵为
,接收符号Y={0,1,2,3},其失真矩阵为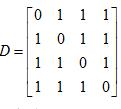 ,求Dmax和Dmin。
,求Dmax和Dmin。
正确答案

答案解析
略
相似试题
(简答题)
有一个二元对称信道,其信道矩阵为。设该信源以1500bit/s的速度传输输入符号。现有一消息序列共有14000个二元符号,并设p(0)=p(1)=1/2,问从信息传输的角度来考虑,10秒钟内能否将这消息序列无失真地传递完?
(简答题)
设信源通过一干扰信道,接收符号为Y={b1,b2},信道传递矩阵为,求 (1)信源X中事件a1和a2分别含有的自信息量。 (2)收到消息bj(j=1,2)后,获得的关于ai(i=1,2)的信息量。 (3)信源X和信宿Y的信息熵。 (4)信道疑义度H(X/Y)和噪声熵H(Y/X)。 (5)接收到信息Y后获得的平均互信息量。
(简答题)
设有一个信源,它产生0,1序列的信息。它在任意时间而且不论以前发生过什么符号,均按p(0)=0.4,p(1)=0.6的概率发出符号。 (1)试问这个信源是否是平稳的? (2)试计算及; (3)试计算H(X4)并写出X4信源中可能有的所有符号。
(单选题)
有一二进制信源符号,0和1发生的概率分别P(0)与P(1),当()概率发生时,信源的熵达到最大值。
(简答题)
一阶马尔可夫信源的状态图如图所示。信源X的符号集为{0,1,2}。 (1)求平稳后信源的概率分布; (2)求信源的熵H∞。
(简答题)
信源空间为: 码符号为X={0,1,2},试构造一种三元的紧致码。
(简答题)
一个马尔可夫信源有3个符号{u1,u2,u3},转移概率为:p(u1|u1)=1/2,p(u2|u1)=1/2,p(u3|u1)=0,p(u1|u2)=1/3,p(u2|u2)=0,p(u3|u2)=2/3,p(u1|u3)=1/3,p(u2|u3)=2/3,p(u3|u3)=0,画出状态图并求出各符号稳态概率。
(简答题)
某一无记忆信源的符号集为{0,1},已知P(0)=1/4,P(1)=3/4。 (1)求符号的平均熵; (2)有100个符号构成的序列,求某一特定序列(例如有m个“0”和(100 - m)个“1”)的自信息量的表达式; (3)计算(2)中序列的熵。
(简答题)
设离散无记忆信源其失真度为汉明失真度。 (1)求Dmin,R(Dmin),并写出相应试验信道的信道矩阵; (2)求Dmax,R(Dmax),并写出相应试验信道的信道矩阵; (3)若允许平均失真度D=1/3,试问信源的每一个信源符号平均最少由几个二进制码符号表示?


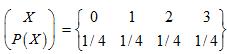 ,接收符号Y={0,1,2,3},其失真矩阵为
,接收符号Y={0,1,2,3},其失真矩阵为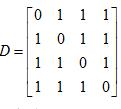 ,求Dmax和Dmin。
,求Dmax和Dmin。 