
(简答题)
设信源 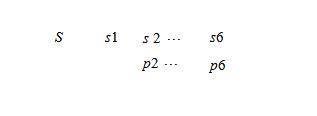 将此信源编码为r元惟一可译变长码(即码符号集X={1,2,r}),其对应的码长为(l1,l2,l6)=(1,1,2,3,2,3),求r值的下限。
将此信源编码为r元惟一可译变长码(即码符号集X={1,2,r}),其对应的码长为(l1,l2,l6)=(1,1,2,3,2,3),求r值的下限。
正确答案

答案解析
略
相似试题
(简答题)
设有两个信源X和Y如下: (1)分别用霍夫曼码编成二元变长惟一可译码,并计算其编码效率; (2)分别用香农编码法编成二元变长惟一可译码,并计算编码效率; (3)分别用费诺编码方法编成二元变长惟一可译码,并计算编码效率; (4)从X、Y两种不同信源来比较这三种编码方法的优缺点。
(简答题)
若有一信源 每秒钟发出2.66个信源符号。将此信源的输出符号送入某一个二元信道中进行传输(假设信道是无噪无损的),而信道每秒钟只传递两个二元符号。试问信源不通过编码能否直接与信道连接?若通过适当编码能否中在信道中进行无失真传输?若能连接,试说明如何编码并说明原因。
(简答题)
设信源求此信源的熵,并解释为什么H(X)>log6,不满足信源熵的极值性。
(简答题)
解释无失真变长信源编码定理。
(简答题)
简述Shannon第一定理—离散无失真信源编码定理(定长和变长)及含义。
(简答题)
考虑一个信源概率为{0.35,0.20,0.15,0.15,0.10,0.10,0.05,0.05}的DMS。给出此信源的霍夫曼码。
(简答题)
一个DMS只有三个输出符号,它们的概率为{0.5,0.4,0.1}。 (1)给出此信源的霍夫曼码并确定编码效率。 (2)每次考虑两个符号时,给出此信源的霍夫曼码并确定编码效率。 (3)每次考虑三个符号时,给出此信源的霍夫曼码并确定编码效率。
(简答题)
考虑一个信源的概率为{0.35,0.25,0.20,0.15,0.05}的DMS。 (1)给出此信源的霍夫曼码。 (2)计算出这些码子的平均码长。 (3)这个码的效率η是多少?
(简答题)
设离散无记忆信源其失真度为汉明失真度。 (1)求Dmin,R(Dmin),并写出相应试验信道的信道矩阵; (2)求Dmax,R(Dmax),并写出相应试验信道的信道矩阵; (3)若允许平均失真度D=1/3,试问信源的每一个信源符号平均最少由几个二进制码符号表示?


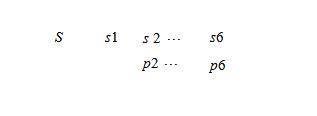 将此信源编码为r元惟一可译变长码(即码符号集X={1,2,r}),其对应的码长为(l1,l2,l6)=(1,1,2,3,2,3),求r值的下限。
将此信源编码为r元惟一可译变长码(即码符号集X={1,2,r}),其对应的码长为(l1,l2,l6)=(1,1,2,3,2,3),求r值的下限。 