(单选题)
球面上有3个点,其中任意两点的球面距离都等于大圆周长的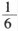 ,经过3个点的小圆的周长为4π,那么这个球的半径为()。
,经过3个点的小圆的周长为4π,那么这个球的半径为()。
A4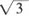
B2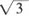
C2
D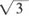
正确答案
答案解析

相似试题
(单选题)
长方体的一个顶点上的三条棱分别是3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是()。
(单选题)
已知球面上过A、B、C三点的截面到球心的距离是球半径的一半,且AB=BC=CA=2,则球表面积是()。
(单选题)
一导体球外充满相对介电常数为εr的均匀电介质,若测得导体表面附近场强为E,则导体球面上的自由电荷面密度σ为()
(简答题)
如图,过半径为R的球面上一点P作三条两两垂直的弦PA、PB、PC。 (1)求证:PA2+PB2+PC2为定值; (2)求三棱锥P-ABC的体积的最大值。
(简答题)
四面体的顶点和各棱的中点共10个点。 (1)设一个顶点为A,从其他9点中取3个点,使它们和点A在同一平面上,不同的取法有多少种? (2)在这10点中取4个不共面的点,不同的取法有多少种?
(简答题)
信息技术课堂教学中,经常会使用任务驱动法,教师在设计这些任务时需要注意些什么?请答出其中两点。
(简答题)
针对“点到直线的距离公式”,有两位老师分别设计了以下两个教学片段。请你分析哪一个教学情境更好。 (一)师:一条河的两岸可以看成平行的直线,某人在岸边要驾驶船到对岸,请问,他应该选择在哪个位置到对岸,才能以最短的路径实现目的? 生:随便那个位置都可以,因为岸的一边上任意点到对岸的距离都相等。 师:为什么? 生:感觉。 师:这种感觉很好,但我们应该给予证明。今天,我们就来学习点到直线的距离公式。 …… (二)师:前面我们学习了平面上两直线的位置关系:平行与相交。当两直线相交时,我们采用角来刻画它们的“相交程度”。那么,如果两直线平行时,我们采用什么方法来刻画呢?(师平行地拿两支笔进行远近移动) 生:距离。 师:什么意思? 生:你刚才在比划,给我们一个感觉,两平行直线有远和近的区别。 师:好,那么怎样刻画两直线的距离呢? 生甲:作任意一条直线与两直线都垂直,被它们所截得的线段长度都相等,这个长度我们就定义为两平行线的距离。 师:很好!但要说明怎么作任意直线与两直线都垂直,还有别的什么方法? 生乙:其实,两平行直线上的一点到另一条直线的距离相等,这个距离可以定义为两平行直线间的距离。 师:很好!为了研究两平行直线的距离,我们可以选择甲和乙的办法,大家看,该选择哪个办法? 生丙:选择甲,因为点到点的距离最原始。 生丁:选择乙,因为点到直线的距离也是通过点到点的距离来刻画的,如果能够得到点到直线的距离,可以少走弯路。 师:两位同学的构思都有道理,那么,我们就合二为一。今天,我们就开始学习点到直线的距离。 ……
(简答题)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1。 (1)求椭圆C的标准方程; (2)若直线Z:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证:直线l过定点,并求出该定点的坐标。
(单选题)
Flash MX的舞台上有同一个图形元件的两个实例,改变其中一个实例的颜色和大小,另外一个实例()。


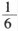 ,经过3个点的小圆的周长为4π,那么这个球的半径为()。
,经过3个点的小圆的周长为4π,那么这个球的半径为()。 