
(简答题)
设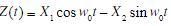 是一随机过程,若X2和X2是彼此独立且具有均值为0、方差
是一随机过程,若X2和X2是彼此独立且具有均值为0、方差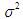 为的正态随机变量,试求: (1)
为的正态随机变量,试求: (1) 、
、 ; (2)Z(t)的一维分布密度函数f(z); (3)
; (2)Z(t)的一维分布密度函数f(z); (3)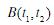 和
和 。
。
正确答案

答案解析
略
相似试题
(填空题)
若吸收剂入塔浓度X2降低,其它操作条件不变,则出口气体浓度()。
(单选题)
连续采样读入三个信号X1、X2、X3,且X1
(填空题)
多变量异或运算时,若x1⊕x2⊕...⊕xn=0,则xi=1的个数必为()个。(奇或偶)
(单选题)
如果X是原子,X2是实际存在的分子,反应X2(g)━━2X(g)的△rH应该是()
(填空题)
在吸收塔调节过程中,如减小液体的进口浓度x2,则吸收推动力增大,传质速率增加,吸收比提高,则气体出口浓度y2(),液体出口浓度()
(填空题)
均方值Ψx2表示的是信号的强度,它与均值μx、方差σx2的关系是()。
(单选题)
某事故树的最小割集为:{x1} {x2,x3}{x2,x4}{x2,x5},其结构重要度是()。
(简答题)
求正弦信号的均值ux、均方值ψx2和概率密度函数p(x)。
(简答题)
x1(n)=R3(n),x2(n)=R5(n),计算x1(n)*x2(n)。


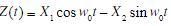 是一随机过程,若X2和X2是彼此独立且具有均值为0、方差
是一随机过程,若X2和X2是彼此独立且具有均值为0、方差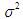 为的正态随机变量,试求: (1)
为的正态随机变量,试求: (1) 、
、 ; (2)Z(t)的一维分布密度函数f(z); (3)
; (2)Z(t)的一维分布密度函数f(z); (3)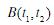 和
和 。
。 