(单选题)
设A是3阶矩阵,P=(α1,α2,α3)是3阶可逆矩阵,且,若矩阵Q=(α1,α2,α3),则Q-1AQ=()。
A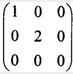
B
C
D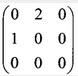
正确答案
答案解析
略
相似试题
(单选题)
已知3维列向量α,β满足αTβ=3,设3阶矩阵A=βαT,则()。
(单选题)
已知λ=2是三阶矩阵A的一个特征值,α1,α2是A的属于λ=2的特征向量。若α1=(1,2,0)T,α2=(1,0,1)T,向量β=(-1,2,-2)T,则Aβ等于()。
(单选题)
设向量组A:α1=(1,0,5,2),α2=(-2,1,-4,1),α3=(-1,1,t,3),α4=(-2,1,-4,1)线性相关,则t必定等于().
(单选题)
设向量组A:α1=(1,-1,0),α2=(2,1,t),α3=(0,1,1)线性相关,则t等于()。
(单选题)
设向量组A:α1=(t,1,1),α2=(1,t,1),α3=(1,1,t)的秩为2,则t等于().
(单选题)
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()。
(单选题)
设α,β,γ均为三维列向量,以这三个向量为列构成的3阶方阵记为A,即A=(αβγ)。若α,β,γ所组成的向量组线性相关,则|A|的值是()。
(单选题)
设α1,α2,α3,β是n维向量组,已知α1,α2,β线性相关,α2,α3,β线性无关,则下列结论中正确的是()。
(单选题)
3维向量组A:α1,α2,…,αM线性无关的充分必要条件是().


