
(简答题)
波动方程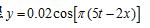 (SI制),求 (1)波的振幅,角频率,周期, 波速,波长,频率? (2)求x=0.2m处的质点,在t=1s时的相位,它是原点处质点在哪一刻的相位?
(SI制),求 (1)波的振幅,角频率,周期, 波速,波长,频率? (2)求x=0.2m处的质点,在t=1s时的相位,它是原点处质点在哪一刻的相位?
正确答案

答案解析
略
相似试题
(填空题)
一平面简谐波的波动方程为(SI制),则它的振幅为()、角频率为()、周期为()、波速为()、波长为()。
(填空题)
一横波的波动方程是y=0.02cos2π(100t–0.4X)(SI制)则振幅是(),波长是(),频率是(),波的传播速度是()。
(简答题)
设一简谐振动其方程为(SI制),求: (1)振动的振幅、频率和初相位; (2)t=2.0 s时的位移、速度和加速度。
(简答题)
一平面简谐波沿x轴正向传播,如图所示,已知振幅为A,频率为v,波速为u, (1)若t=0时,原点O处质元正好由平衡位置向位移正方向运动,写出此波的波动方程; (2)若从分界面反射的波的振幅与入射波振幅相等,试写出反射波的波动方程,并求x轴上因入射波与反射波干涉而静止的各点的位置。
(单选题)
一简谐波沿x轴正向传播,波的振幅为A,角频率为ω,波速为u。若以原点处的质元经平衡位置正方向运动时作为计时的起点,则该波的波动方程是()。
(简答题)
图示一平面简谐波在t=0时刻的波形图,求 (1)该波的波动表达式; (2)P处质点的振动方程。
(简答题)
若简谐运动方程为,求: (1)振幅、频率、角频率、周期和初相; (2)t=2s时的位移、速度和加速度.
(简答题)
抛物线形弯管的表面光滑,可绕竖直轴以匀角速率转动,抛物线方程为y=ax∧2,a为常数,小环套与弯管上。求 (1)弯管角速度多大? (2)若为圆形光滑弯管,情形如何?
(简答题)
某质点作简谐振动,周期为2s,振幅为0.06m,开始计时(t=0),质点恰好处在负向最大位移处,求: (1)该质点的振动方程; (2)此振动以速度u=2m/s沿x轴正方向传播时,形成的一维筒谐波的波动方程(以该质点的平衡位置为坐标原点); (3)该波的波长。


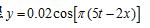 (SI制),求 (1)波的振幅,角频率,周期, 波速,波长,频率? (2)求x=0.2m处的质点,在t=1s时的相位,它是原点处质点在哪一刻的相位?
(SI制),求 (1)波的振幅,角频率,周期, 波速,波长,频率? (2)求x=0.2m处的质点,在t=1s时的相位,它是原点处质点在哪一刻的相位? 