其中λ>0为未知参数，x1，x2，...，xn是一组样本值，求参数λ的最大似然估计。 
（简答题）
设总体X服从参数为λ的泊松分布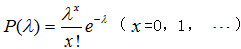 
其中λ>0为未知参数，x1，x2，...，xn是一组样本值，求参数λ的最大似然估计。
正确答案
答案解析
略
相似试题
（简答题）
设随机变量X，Y相互独立，且分别服从参数为λ1和型λ2的泊松分布， （1）证明：X+Y服从参数为λ1+λ2的泊松分布； （2）对给定的X+Y，X的条件分布是二项分布：
（填空题）
设随机变量X服从λ=2泊松分布，则=（）
（单选题）
设X服从参数为λ>0的泊松分布，其方差DX=（）
（填空题）
设随机变量X服从参数为2的泊松分布，则E（2X）=（）
（单选题）
设X服从参数为λ>0的泊松分布，其数学期望EX=（）
（填空题）
设随机变量X服从参数为λ的泊松（Poisson）分布，且已知E[（X-1）（X-2）]=1＝1，则λ=（）。
（单选题）
设随机变量X服从参数为的泊松分布，且则的值为（）.
（简答题）
设总体X的密度函数为，其中λ＞0为未知参数，X1，X2，...Xn为来自总体的一组样本 求： （1）λ的矩估计量； （2）λ的最大似然估计量。
（简答题）
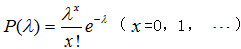设总体X的概率密度函数是 λ>0为未知参数，x1，x2，...，xn是一组样本值，求参数λ的最大似然估计。
