
(简答题)
设总体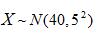 (1)抽取容量为36的样本,求样本平均值
(1)抽取容量为36的样本,求样本平均值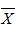 在38与43之间的概率; (2)抽取容量为64的样本,求
在38与43之间的概率; (2)抽取容量为64的样本,求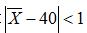 的概率; (3)抽取样本容量n多大时,才能使概率
的概率; (3)抽取样本容量n多大时,才能使概率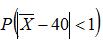 达到0.95?
达到0.95?
正确答案

答案解析
略
相似试题
(简答题)
设总体,总体,从总体X中抽取容量为10的样本,其样本方差计为;从总体Y中抽取容量为8的样本,其样本方差记为,求下列概率: (1) (2)
(简答题)
设总体从总体X中抽取容量为10的样本,从总体Y中抽取容量为8的样本,求下列概率:
(简答题)
设总体X~N(50,62),Y~N(46,42),从总体X中抽取容量为10的样本,从总体Y中抽取容量为8的样本,求概率
(简答题)
设总体X~N(μ,σ2)中抽取容量为16的一个样本,样本方差S2=0.07,试求总体方差的置信度为0.95的置信区间。
(简答题)
设总体要使总体均值μ的置信水平为1-α的置信区间的长度不大于l,问需要抽取多大容量的样本?
(简答题)
设总体X服从均值为1/2的指数分布,X1,X2,X3,X4是来自总体的容量为4的样本,求
(简答题)
从总体X服从正态分布N(μ,σ2)中抽取容量为10的一个样本,样本方差S2=0.07,试求总体方差σ2的置信度为0.95的置信区间。
(简答题)
设总体是来自的容量为3的样本,求
(简答题)
设总体是来自X的容量为3的样本,求


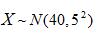 (1)抽取容量为36的样本,求样本平均值
(1)抽取容量为36的样本,求样本平均值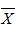 在38与43之间的概率; (2)抽取容量为64的样本,求
在38与43之间的概率; (2)抽取容量为64的样本,求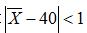 的概率; (3)抽取样本容量n多大时,才能使概率
的概率; (3)抽取样本容量n多大时,才能使概率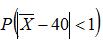 达到0.95?
达到0.95? 