
(简答题)
设Yt=β0+β1D1+β2D2+β4Xt+ut,其中,Y=大学教师收入,X=教学年份, 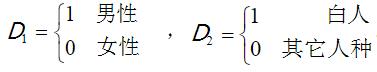 求E(Yt∣D1=1,D2=1,Xt),并解释其意义。
求E(Yt∣D1=1,D2=1,Xt),并解释其意义。
正确答案

答案解析
略
相似试题
(单选题)
在模型中Yt=β0+β1Xt+β2Xt-1+…βkXt-k-1+μt中,系数β1为()。
(单选题)
设消费函数为Yi=β0+β1D+β2Xi+ui,式中Yi=第i个居民的消费水平,Xi=第i个居民的收入水平,D为虚拟变量,D=1表示正常年份,D=0表示非正常年份,则()
(简答题)
设消费函数为Yt=β0+β1Xt+ut,若月收入Xt在1000元以内和1000元以上的边际消费倾向存在显著差异,如何修改原来的模型?
(简答题)
设有限分布滞后模型为Yt=α+β0Xt+β1Xt-1+β2Xt-2+β3Xt-3+β4Xt-4+ut,假设用2阶多项式变换该模型为阿尔蒙多项式模型,使用普通最小二乘法估计这个模型,得到: 求X对Y的短期影响乘数、长期影响乘数和延期影响乘数。
(单选题)
在线性到对数模型,LnYt=β1+β2t+ut中,Yt代表国内生产总值,t代表时间变量,则斜率系数β2代表()
(单选题)
在模型Yt=β1+β2X2t+β3X3t+μt的回归分析结果中,有F=263489.23,F的p值=0.000000,则表明()。
(单选题)
若假定影响被解释变量Yt的因素不是Xt而是Xt+1的预期X*t+1,即Yt=β0+β1X*t+1+ut,建立在这种经济理论基础上的模型属于()
(多选题)
设消费函数为Yi=β0+β1D+β2Xi+ui,Yi=第i个居民的消费水平,Xi=第i个居民的收入水平,D为虚拟变量,该模型为()
(简答题)
对于模型:Yt=β1β2Xt+μt。


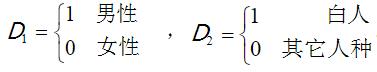 求E(Yt∣D1=1,D2=1,Xt),并解释其意义。
求E(Yt∣D1=1,D2=1,Xt),并解释其意义。 