求 （1）棒与两球构成的系统在时刻t对z轴的角动量； （2）在t＝0时系统所受外力对z轴的合外力矩. 
（简答题）
如图所示，一长为2l的细棒AB，其质量不计，它的两端牢固地联结着质量各为m的小球，棒的中点O焊接在竖直轴z上，并且棒与z轴夹角成α角.若棒在外力作用下绕z轴（正向为竖直向上）以角直速度ω＝ω0（1－e－t）转动，其中ω0为常量.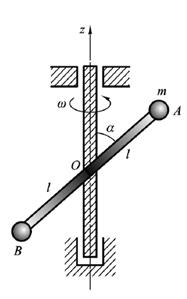 
求 （1）棒与两球构成的系统在时刻t对z轴的角动量； （2）在t＝0时系统所受外力对z轴的合外力矩.
正确答案
答案解析
略
相似试题
（简答题）
如图所示，一长为2l的细棒AB，其质量不计，它的两端牢固地联结着质量各为m的小球，棒的中点O焊接在竖直轴z上，并且棒与z轴夹角成α角.若棒在外力作用下绕z轴（正向为竖直向上）以角直速度ω＝ω0（1－e－t）转动，其中ω0为常量.求（1）棒与两球构成的系统在时刻t对z轴的角动量；（2）在t＝0时系统所受外力对z轴的合外力矩.
（简答题）
求均匀带电的细棒在（1）通过自身端点并垂直于棒的平面上，（2）自身的延长线上的场强分布，设棒长为2l，电量为q.
（简答题）
有一长为l的细绳，以张力T固定在两端，设在位置x0处，挂着一质量Mm，如图所示，试问： （1）当质量被垂直拉离平衡位置时，它所受到的恢复平衡的力由何产生？并应怎样表示？ （2）当外力去掉后，质量Mm在此恢复力作用下产生振动，它的振动频率应，如何表示？ （3）当质量置于哪一位置时，振动频率最低？
（简答题）
一根质量为m、长为l的均匀细棒，在竖直平面内绕通过其一端并与棒垂直的水平轴转动，如图所示。现使棒从水平位置自由下摆，求： （1）开始摆动时的角加速度； （2）摆到竖直位置时的角速度。
（单选题）
一长为l，质量为m 的匀质细棒，绕一端作匀速转动，其中心处的速率为v，则细棒的转动动能为（）。
（简答题）
两根相同的长为l带电细棒，线电荷密度为λ，其放置如图所示，假设棒上的电荷不能自由移动，求两棒之间的静电作用力。
（简答题）
一长为l、质量为m的均匀细棒，在光滑的平面上绕质心作无滑动的转动，其角速度为ω.若棒突然改绕其一端转动，求：（1）以端点为转轴的角速度ω′；（2）在此过程中转动动能的改变.
（简答题）
如图所示，光滑水平桌面上，长为H质量为m1的均匀细棒能绕一端自由转动.开始时，细棒静止于水平桌面上.现有长度为r=H/2的轻质细线牵引质量为m2的小球，在水平桌面内以速度v20垂直撞击细棒并粘在一起.细线的固定点与细棒的转轴近似重合.求细棒和小球一起运动时的角速度Ω。
（简答题）
两小球的质量都是m，都用长为I的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2θ，如图所示，设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量。
