
(简答题)
已知均质杆OB=AB=l,质量均为m,在铅垂面内运动,AB杆上作用一不变的力偶矩M,系统初始静止,不计摩擦。求当端点A运动到与端点O重合时的速度。 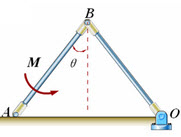
正确答案

答案解析
略
相似试题
(简答题)
已知均质杆AB的质量m=4kg,长l=600mm,均匀圆盘B的质量为6kg,半径为r=600mm,作纯滚动。弹簧刚度为k=2N/mm,不计套筒A及弹簧的质量。连杆在与水平面成30º角时无初速释放。求(1)当AB杆达水平位置而接触弹簧时,圆盘与连杆的角速度;(2)弹簧的最大压缩量δmax
(单选题)
均质细直杆AB长为l,质量为m,以匀角速度ω绕O轴转动,如图所示,则AB杆的动能为:()
(单选题)
图示均质等截面直杆,质量为m,长为l,已知,则的计算公式为()。
(单选题)
图示均质圆盘质量为m,绕固定轴O转动,角速度均为w。动能为()。
(简答题)
两个均质杆AB和BC分别重P1和P2,其端点A和C用球铰固定在水平面,另一端B由球铰链相连接,靠在光滑的铅直墙上,墙面与AC平行,如图所示。如AB与水平线的交角为45º,∠BAC=90º,求A和C的支座约束力以及墙上点B所受的压力。
(单选题)
图示曲柄连杆机构中,OA=r,AB=2r,OA、AB及滑块B质量均为m,曲柄以ω的角速度绕O轴转动,则此时系统的动能为:()
(单选题)
杆AB长为l,质量为m,图示瞬时点A处的速度为v,则杆AB的动量大小为:()
(简答题)
已知:轮O的半径为R1,质量为m1,质量分布在轮缘上;均质轮C的半径为R2,质量为m2,与斜面纯滚动,初始静止。斜面倾角为θ,轮O受到常力偶M驱动。求:轮心C走过路程s时的速度和加速度。
(单选题)
半径为R、质量为m的均质圆轮沿斜面作纯滚动如图所示。已知轮心C的速度为v、加速度为a,则该轮的动能为()



