
(简答题)
质量m的物体从静止开始,在竖直平面内沿着固定的四分之一圆周从A滑到B。在B处时,物体速度的大小为vB。已知圆的半径为R,求物体从A滑到B的过程中摩擦力所作的功: (1)用功的定义求; (2)用动能定理求; (3)用功能原理求。 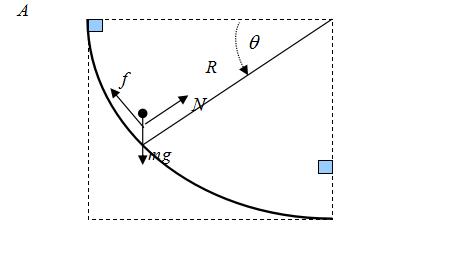
正确答案

答案解析
略
相似试题
(简答题)
一轻绳绕于半径为R的圆盘边缘,在绳端施以F=mg的拉力,圆盘可绕水平固定光滑轴在竖直平面内转动。圆盘质量为M,并从静止开始转动。
(简答题)
一轻绳绕于半径为R的圆盘边缘,在绳端施以F=mg的拉力,圆盘可绕水平固定光滑轴在竖直平面内转动。圆盘质量为M,并从静止开始转动。
(简答题)
一轻绳绕于半径为R的圆盘边缘,在绳端施以F=mg的拉力,圆盘可绕水平固定光滑轴在竖直平面内转动。圆盘质量为M,并从静止开始转动。
(简答题)
如图示,一均匀细棒,长为l,质量为m,可绕过棒端且垂直于棒的光滑水平固定轴O在竖直平面内转动,棒被拉到水平位置从静止开始下落,当它转到竖直位置时,与放在地面上一静止的质量亦为m的小滑块碰撞,碰撞时间极短,小滑块与地面间的摩擦系数为μ,碰后滑块移动距离S后停止,而棒继续沿原转动方向转动,直到达到最大摆角。求:碰撞后棒的中点C离地面的最大高度h。
(填空题)
质量为m、长为l的棒,可绕通过棒中心且与棒垂直的竖直光滑固定轴O在水平面内自由转动(转动惯量J=ml2/12),开始时棒静止,现有一子弹,质量也是m,在水平面内以速度v0垂直射入棒端并嵌在其中,则子弹嵌入后棒的角速度ω=()。
(填空题)
质量为m、长为l的棒,可绕通过棒中心且与棒垂直的竖直光滑固定轴O在水平面内自由转动(转动惯量J=ml2/12)开始时棒静止,现有一子弹,质量也是m,在水平面内以速度v0垂直射入棒端并嵌在其中则子弹嵌入后棒的角速度ω=()。
(填空题)
质量为m,长为l的匀质细杆,可绕过其端点的水平轴在竖直平面内自由转动。如果将细杆置与水平位置,然后让其由静止开始自由下摆,则开始转动的瞬间,细杆的角加速度为(),细杆转动到竖直位置时角速度为()。(已知此匀质细杆转动惯量为)
(简答题)
一长l=0.40m的均匀木棒,质量M=1.00kg,可绕水平轴O在竖直平面内转动,开始时棒自然地竖直悬垂。现有质量m=8g的子弹以v=200m/s的速率从A点与O点的距离为,如图。 求: (1)棒开始运动时的角速度; (2)棒的最大偏转角。
(简答题)
如图所示,一劲度系数为k的轻弹簧,竖直悬挂一质量为m的物体后静止,再把物体向下拉,使弹簧伸长后开始释放,判断物体是否作简谐振动?



