（单选题）
若F′（x）=f（x），即F（x）是f（x）的一个原函数，则下列等式中哪一个可以成立？（）
A
F′（x）dx=f（x）+c
B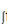
f（x）dx=F（x）+c
C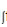
F（x）dx=f（x）+c
D
f′（x）dx=F（x）+c
正确答案
答案解析
f（x）dx表示求f（x）全体原函数，只需求出一个原函数加c。由已知条件知，F（x）是f（x）的一个原函数，故加c可得答案B。 相似试题
（判断题）
若f(x)在[a,b]上可积，则f(x)在[a,b]上连续。
（判断题）
若f（x）在x0点可指导，则丨f（x）丨也在x0点可指导。
（单选题）
若f′（x）=g′（x），则下列哪个式子成立（）？
（单选题）
若f′（cos2x）=sinx，则f（x）等于：（）
（判断题）
若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.
（单选题）
若f（x）dx=F（x）+c，则sinxf（cosx）dx等于：（）
（判断题）
若z=f(x,y)在（x0,y0）处的两个一阶偏导数存在，则函数z=f(x,y)在(x0,y0)处可微
（单选题）
设f（x）、f′（x）为已知的连续函数，则微分方程y′+f′（x）y=f（x）f′（x）的通解是：（）
（单选题）
设f′（lnx）=1+x，则f（x）等于（）
