
(简答题)
已知直线l:ax+y=1在矩阵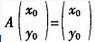 对应的变换作用下变为直线l′:x+by=1。 (1)求实数a,b的值; (2)若点P(x0,y0),在直线l上,且
对应的变换作用下变为直线l′:x+by=1。 (1)求实数a,b的值; (2)若点P(x0,y0),在直线l上,且 ,求点P的坐标。
,求点P的坐标。
正确答案

答案解析
略
相似试题
(简答题)
已知矩阵,且。 (Ⅰ)求实数a、b、c、d的值; (Ⅱ)求直线y=3x在矩阵M所对应的线性变换作用下的像的方程。
(简答题)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1。 (1)求椭圆C的标准方程; (2)若直线Z:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证:直线l过定点,并求出该定点的坐标。
(简答题)
已知定点P(6,4)与定直线l1:y=4x,过P点的直线l与l1交于第一象限Q点,与x轴正半轴交于点M,求使△OQM面积最小的直线l方程。
(简答题)
函数y=x2-2ax+1,若它的增区间是[2,+∞),则a的取值是多少?若它在区间[2,+∞)上递增,则a的取值范围是什么?
(简答题)
在平面直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系。已知点A的极坐标为,直线l的极坐标方程为,且点A在直线l上。 (1)求α的值及直线ι的直角坐标方程: (2)圆c的参数方程为,试判断直线l与圆C的位置关系。
(单选题)
设直线的方程是Ax+By=0,从1,2,3,4,5这五个数中每次取两个不同的数作为A、B的值,则所得不同直线的条数是()。
(简答题)
已知曲线x2+2y2+4x+4y+4=0按向量a=(2,1)平移后得到曲线C。 (1)求曲线C的方程; (2)过点D(0,2)的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设,求实数λ的取值范围。
(单选题)
对任意的实数k,直线y-2=k(x+1)恒过定点M,则M的坐标是()。
(单选题)
已知实数x、y满足x2+y2=1,则(1-xy)(1xy)()。


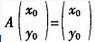 对应的变换作用下变为直线l′:x+by=1。 (1)求实数a,b的值; (2)若点P(x0,y0),在直线l上,且
对应的变换作用下变为直线l′:x+by=1。 (1)求实数a,b的值; (2)若点P(x0,y0),在直线l上,且 ,求点P的坐标。
,求点P的坐标。 