
(简答题)
一工厂生产的某种元件的寿命X(以小时计)服从均值μ=160,均方差为σ的正态分布,若要求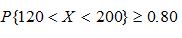 允许最大为多少?
允许最大为多少?
正确答案

答案解析
略
相似试题
(简答题)
某种型号的电子的寿命X(以小时计)具有以下的概率密度: 现有一大批此种管子(设各电子管损坏与否相互独立)。任取5只,问其中至少有2只寿命大于1500小时的概率是多少?
(简答题)
设某种型号的电子管的寿命(以小时计)近似地服从N(160,202)分布.随机地选取4只,求其中没有一只寿命小于180的概率.
(简答题)
一工厂生产某种设备的寿命X(以年计)服从指数分布,概率密度为 为确保消费者的利益,工厂规定出售的设备若在一年内损坏可以调换.若售出一台设备,工厂获利100元,而调换一台则损失200元,试求工厂出售一台设备赢利的数学期望.
(简答题)
一工厂生产的电子管寿命X(小时)服从正态分布N(160,σ2),若要求P{120<X≤200}≥0.8,允许σ最大不超过多少?
(简答题)
一工厂生产的某种设备的寿命X(以年计)服从指数分布,概率密度为工厂规定出售的设备若在一年内损坏,可予以调换。若工厂出售一台设备可赢利100元,调换一台设备厂方需花费300元。试求厂方出售一台设备净赢利的数学期望。
(简答题)
一工厂生产的某种设备的寿命X(以年计)服从指数分布,概率密度为 工厂规定,出售的设备若在售出一年之内损坏可予以调换.若工厂售出一台设备赢利100元,调换一台设备厂方需花费300元.试求厂方出售一台设备的平均净赢利。
(简答题)
一制造商声称他的工厂生产的某种牌号的电池的寿命的方差为5000(小时2),为了检验这一主张,随机地取26只电池测得样本方差为7200小时2,有理由认为样本来自正态总体。现需取α=0.02检验假设
(简答题)
某种电子元件的寿命X是随机变量,其概率密度为 求(1)常数C; (2)若将3个这种元件串联在一条线路上,试计算该线路使用150小时后仍能正常工作的概率。
(简答题)
某公司生产电子元件,其寿命分布近似服从正态分布。该公司声称:某种型号电子元件的平均寿命高于3000小时。现在从该公司的这种电子元件中抽取了5个,它们的寿命分别为: 2980,3020,3010,3010,2990。问在显著性水平α=0.05下,能否接受该公司的声称。


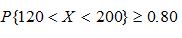 允许最大为多少?
允许最大为多少? 