
(简答题)
某种电子元件的寿命X是随机变量,其概率密度为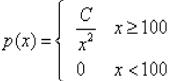 求(1)常数C; (2)若将3个这种元件串联在一条线路上,试计算该线路使用150小时后仍能正常工作的概率。
求(1)常数C; (2)若将3个这种元件串联在一条线路上,试计算该线路使用150小时后仍能正常工作的概率。
正确答案

答案解析
略
相似试题
(简答题)
某种电子元件的寿命X(以年计)服从数学期望为2的指数分布,各元件的寿命相互独立。随机取100只元件,求这100只元件的寿命之和大于180的概率。
(简答题)
设某种型号的电子管的寿命(以小时计)近似地服从N(160,202)分布.随机地选取4只,求其中没有一只寿命小于180的概率.
(简答题)
设某种商品一周的需要量是一个随机变量,其概率密度为 并设各周的需要量是相互独立的
(简答题)
设某种商品一周的需要量是一个随机变量,其概率密度为 并设各周的需要量是相互独立的
(简答题)
设一圆的半径X是随机变量,其概率密度为 求圆面积A的概率密度。
(简答题)
某种型号的电子的寿命X(以小时计)具有以下的概率密度: 现有一大批此种管子(设各电子管损坏与否相互独立)。任取5只,问其中至少有2只寿命大于1500小时的概率是多少?
(简答题)
设某种商品一周的需要量是一个随机变量,其概率密度为 并设各周的需要量是相互独立的 试求三周的需要量的概率密度。
(简答题)
设某种商品一周的需要量是一个随机变量,其概率密度为 并设各周的需要量是相互独立的
(填空题)
已知随机变量X只能取-1,0,1,2四个数值,其相应的概率依次是,则c=()


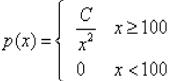 求(1)常数C; (2)若将3个这种元件串联在一条线路上,试计算该线路使用150小时后仍能正常工作的概率。
求(1)常数C; (2)若将3个这种元件串联在一条线路上,试计算该线路使用150小时后仍能正常工作的概率。 