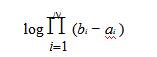(简答题)
N维连续型随机序列X1X2...XN,其各分量幅度分别受限为[ai,bi]。证明:当随机序列的分量各自达到均匀分布并彼此统计独立时熵最大。最大熵为: 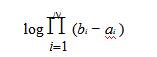
正确答案

答案解析
略
相似试题
(简答题)
N维连续型随机序列X1X2...XN,有概率密度p(X1X2...XN)以及证明:当随机序列的分量各自达到正态分布并彼此统计独立时熵最大。最大熵为:
(简答题)
设信道输入是连续型随机序列X1X2...XN,输出也是连续型随机序列Y1Y2...YN,信道传递概率密度为p(y|x)。试证明: (1)当信源是无记忆时,有 (1)当信源是无记忆时,有
(简答题)
在连续信源中,根据差熵、条件差熵和联合差熵的定义,证明 (1)h(X|Y)≤h(X),当且仅当X和Y统计独立时等号成立; (2)h(X1X2...XN)≤h(X1)+h(X2)+h(XN),当且仅当X1X2...XN彼此统计独立时等式成立。
(简答题)
证明H(X1X2...Xn)≤H(X1)+H(X2)+...+H(Xn)
(简答题)
试证明n维随机变量的共熵,不大于它们各自的熵之和。
(判断题)
N维统计独立均匀分布连续信源的熵是N维区域体积的对数。
(填空题)
对于限峰值功率的N维连续信源,当概率密度()时连续信源熵具有最大值。
(填空题)
已知一个栈的输入序列为1,2,3,...,n,则其输出序列的第2个元素为n的输出序列的种数是()。
(单选题)
若已知一个栈的入栈序列是1,2,3,…,n,其输出序列为p1,p2,p3,…,pn,若p1=n,则pi为()