
(简答题)
在B=0.1T的均匀磁场中,有一个速度大小为v=104m/s的电子沿垂直于B的方向(如图)通过A点,求电子的轨道半径和旋转频率。(基本电荷e=1.60×10-19C,电子质量me=9.11×10-31kg) 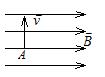
正确答案

答案解析
略
相似试题
(简答题)
如图,一个矩形的金属线框,边长分别为a和b(b足够长).金属线框的质量为m,自感系数为L,忽略电阻.线框的长边与x轴平行,它以速度v0沿x轴的方向从磁场外进入磁感应强度为B0的均匀磁场中,B0的方向垂直矩形线框平面.求矩形线框在磁场中速度与时间的关系式v=v(t)和沿x轴方向移动的距离与时间的关系式x =x(t).
(简答题)
如图,有一弯成θ角的金属架COD放在磁场中,磁感应强度B的方向垂直于金属架COD所在平面,一导体杆MN垂直于OD边,并在金属架上以恒定速度v向右滑动,v与MN垂直,设t=0时,x=0,求下列两情形,框架内的感应电动势εi. (1)磁场分布均匀,且B不随时间改变; (2)非均匀的交变磁场B=Kxcosωt.
(单选题)
如图,一个电量为+q,质量为m的质点,以速度V沿x轴射入磁感应强度为B的均匀磁场中,磁场方向垂直纸面向里,其范围从x=0延伸到无限远,如果质点在x=0和y=0处进入磁场,则它将以速度-V从磁场中某一点出来,这点坐标是x=0和()。
(单选题)
一矩形线框长为a宽为b,置于均匀磁场中,线框绕OO’轴匀角速度w旋转(如图所示)。设t=0时,线框平面处于纸面内,则任一时刻感应电动势的大小为:()
(简答题)
a粒子在磁感应强度为B=0.025T的均匀磁场中沿半径为R=0.83cm的圆形轨道运动。 (1)试计算其德布罗意波长, (2)若使质量m=0.1g的小球以与a粒子相同的速率运动。则其波长为多少?(ma=6.64×10-27kg,h=6.63×10-34J˙s,e=1.6×10-19C)
(单选题)
一矩形线框长为a宽为b,置于均匀磁场中,线框绕OO′轴,以匀角速度旋转(如图所示).设t=0时,线框平面处于纸面内,则任一时刻感应电动势的大小为()
(简答题)
α粒子在磁感应强度为B=0.025T的均匀磁场中沿半径为R=0.83cm的圆形轨道运动.若使质量m=0.1g的小球以与α粒子相同的速率运动.则其波长为多少?(α粒子的质量mα=6.64×10-27kg,普朗克常量h=6.63×10-34J·s,基本电荷e=1.60×10-19C)
(简答题)
磁感应强度为B的均匀磁场只存在于x>0的空间中,且B垂直纸面向内。如图所示,在x=0的平面上有理想边界,一电子质量为m、电荷为-e,它在纸面内以与x=0的界面成60°角的速度v进入磁场,求电子在磁场中的出射点与入射点间的距离。
(简答题)
一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B的方向如图所示。取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t=0)。



