（简答题）

某企业生产一种产品，劳动为唯一可变要素，固定成本既定。短期生产函数Q=-0.1L³+6L2²+12L，求：（1）劳动的平均产量函数和边际产量函数。（2）企业雇用工人的合理范围是多少？（3）若已知劳动的价格为W=480，产品Q的价格为40，则当利润最大时，企业生产多少产品Q？

正确答案

（1）平均产量AP=TP/L= -0.1 L2 +6L+12 边际产量MP=（TP）’= - 0.3 L2+12L+12
（2）企业应在平均产量递减，边际产量为正的生产阶段组织生产，因此雇用工人的数量也应在此范围

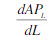＜0，MP＞0内。对AP_L求导，得

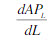= - 0.2 L +6=0。即L=30
当L=30时，AP_L取得最大值，L＞30，AP_L开始递减。令MP_L= - 0.3L²+12L+12=0，得L=40.98
所以，企业雇用工人的合理范围为30≤L≤41
（3）利润π=PQ-WL=40（- 0.1 L³ +6L² +12L）-480L = - 4 L³ +240L² +480L-480L
Π’=- 12L²+480L，当Π’=0时， L=0 （舍去）或L=40.
当L=40时， Π” ＜0，所以L=40,利润π最大。
此时，产量Q= -0.1×40³+6 × 40² +12 × 40 =3680

答案解析

略

相似试题

（单选题）
某企业使用劳动一种可变要素，如果该企业生产的产品价格上升（完全竞争的产品市场），将引起（）
答案解析
（简答题）
计算题：假定某厂商只有一种可变要素劳动L，产出一种产品Q，固定成本为既定，短期生产函数Q=-0。1L3+6L2+12L，求：（1）劳动的平均产量AP为最大值时的劳动人数（2）劳动的边际产量MP为最大值时的劳动人数（3）平均可变成本极小值时的产量
答案解析
（单选题）
假定某印染厂来料加工产品的单价为20元，劳动是该厂唯一的可变投入要素，每工人每天的工资固定为40元。厂商增加劳动的边际产量为“82-4L”，则该厂劳动L每天的最适投入量L为（）人。
答案解析
（简答题）
已知劳动是唯一的可变要素，生产函数为Q＝A＋10L－5L2，产品市场是完全竞争的，劳动价格为W，试说明：（1）厂商对劳动的需求函数。（2）厂商对劳动的需求量与工资反方向变化。（3）厂商对劳动的需求量与产品价格同方向变化。
答案解析
（单选题）
若某企业处于完全竞争的产品市场中经营，其生产要素中A是唯一可变的要素，则该企业对A要素的需求曲线可以由以下何者推出（）
答案解析
（单选题）
如果劳动是唯一的可变生产要素，那么劳动的收益递减意味着（）
答案解析
（单选题）
在劳动作为唯一可变生产要素的情况下，劳动的合理投入区域应该是在（）
答案解析
（判断题）
如果A是产品X生产中唯一的可变投入要素，并且边际产量为MPa=4，要素A的价格Pa=5，则X的边际成本为0.8元。
答案解析
（单选题）
一种可变要素的价格为10美元。该要素的边际产出为5单位的某产品，则能使该完全竞争厂商在此时获得最大利润的产品价格是（）
答案解析