(单选题)
设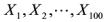 为来自总体
为来自总体 的一个样本,而
的一个样本,而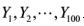 为来自总体
为来自总体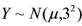 的一个样本,且两个样本独立,以
的一个样本,且两个样本独立,以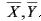 分别表示这两个样本的样本均值,则
分别表示这两个样本的样本均值,则 所服从的分布是()。
所服从的分布是()。
A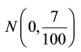
B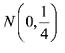
C N(0,7)
DN(0,25)
正确答案
答案解析
略
相似试题
(单选题)
X1,X2,X3设为来自总体X的样本,下列关于E(X)的无偏估计中,最有效的为().
(简答题)
从两个总体中各抽取一个n1=n2=250的独立随机样本,来自总体1的样本比例为p1=40%,来自总体2的样本比例为p2=30%。要求: (1)构造π1-π2的90%的置信区间。 (2)构造π1-π2的95%的置信区间。
(单选题)
假设总体X~,是来自总体的一个样本,为其样本均值,且,则下列成立的是()。
(单选题)
设总体X~N(0,σ2),X1,X2,...Xn(n≥2)是来自该总体的简单随机样本,则σ2的一个无偏估计量是()
(单选题)
来自同一总体的两个样本中,()小的哪个样本均数估计总体均数时更可靠.
(简答题)
设总体X的概率分布律为P{X=i}=1/θ,i=1,2,...,θ,未知参数θ为正整数.X1,X2,...,Xn为来自总体的一组样本,求θ的矩估计量.
(简答题)
设总体X的密度函数为,其中λ>0为未知参数,X1,X2,...Xn为来自总体的一组样本 求: (1)λ的矩估计量; (2)λ的最大似然估计量。
(简答题)
设X1,X2,...Xn是来自总体X的一组简单随机样本,X与S2分别是这组样本的样本均值与样本方差,证明X与S2的如下关系式:
(简答题)
设X1,X2,…,Xn是来自参数为λ的泊松分布总体的一个样本,试求λ的极大似然估计量及矩估计量。


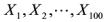 为来自总体
为来自总体 的一个样本,而
的一个样本,而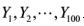 为来自总体
为来自总体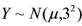 的一个样本,且两个样本独立,以
的一个样本,且两个样本独立,以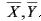 分别表示这两个样本的样本均值,则
分别表示这两个样本的样本均值,则 所服从的分布是()。
所服从的分布是()。 