
(简答题)
证明离散信源有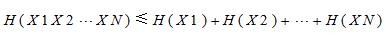 ,并说明等式成立的条件。
,并说明等式成立的条件。
正确答案

答案解析
略
相似试题
(简答题)
证明离散平稳信源有,试说明等式成立的条件。
(简答题)
在连续信源中,根据差熵、条件差熵和联合差熵的定义,证明 (1)h(X|Y)≤h(X),当且仅当X和Y统计独立时等号成立; (2)h(X1X2...XN)≤h(X1)+h(X2)+h(XN),当且仅当X1X2...XN彼此统计独立时等式成立。
(简答题)
设是X=X1,X2,...,XN平稳离散有记忆信源,试证明:
(简答题)
证明一个离散信源在它的输出符号等概率的情况下其熵达到最大值。
(简答题)
试证明:若则 并说明等式的物理意义。
(简答题)
若有三个离散随机变量,有如下关系:X+Y=Z,其中X和Y相互统计独立,试证明: (1)H(X)≤H(Z),当且仅当Y是常量时等式成立; (2)H(Y)≤H(Z),当且仅当X为常量时等式成立; (3)H(Z)≤H(XY)≤H(X)+H(Y),当且仅当X,Y中任意一个为常量时等式成立; (4)I(X;Z)=H(Z)−H(Y); (5)I(XY;Z)=H(Z); (6)I(X;YZ)=H(X); (7)I(Y;Z|X)=H(Y); (8)I(X;Y|Z)=H(X|Z)=H(Y|Z)。
(判断题)
单符号离散信源的联合自信息量和条件自信息量都是非负的和单调递减的。
(简答题)
简述最大离散熵定理。对于一个有m个符号的离散信源,其最大熵是多少?
(判断题)
离散平稳有记忆信源符号序列的平均符号熵随着序列长度L的增大而增大。


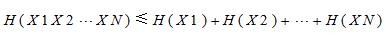 ,并说明等式成立的条件。
,并说明等式成立的条件。 