由(1)图中10倍频程下降了20dB,可直接看出:
ωc=10
(简答题)
将系统的传递函数为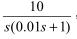 求截止频率ωc
求截止频率ωc
正确答案
答案解析
略
相似试题
(单选题)
二阶系统的传递函数为,则其无阻尼固有频率ωn和阻尼比ξ依次为()。
(简答题)
已知系统单位脉冲响应为g(t)=1-e-t,求传递函数G(s)和频率特性G(jω)。
(判断题)
相位裕量在截止频率ωc处测量。
(填空题)
频率特性G(jω)与传递函数G(s)的关系为()。
(简答题)
系统的闭环传递函数C(s)/R(s)为ωn2/(s2+2ξωns+ωn2)误差定义为e=r-c,试求系统在r(t)为l(t)、tl(t)时的稳态误差。
(填空题)
由传递函数怎样得到系统的频率特性()。
(填空题)
系统的数学模型可以相互转化。由微分方程得到传递函数通过()变换实现。由传递函数到频率特性通过()实现。
(简答题)
已知最小相位系统的开环对数幅频特性L0(ω)和串联校正装置的对数幅频特性Lc(ω)如下图所示,原系统的幅值穿越频率为ωc=24.3rad/s: 1、写出原系统的开环传递函数G0(s),并求其相角裕度γ0,判断系统的稳定性; 2、写出校正装置的传递函数Gc(s); 3、写出校正后的开环传递函数G0(s)Gc(s),画出校正后系统的开环对数幅频特性LGC(ω),并用劳斯判据判断系统的稳定性。
(判断题)
若系统的穿越频率ωc大,则调节速度快,即ts就小。()


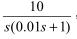 求截止频率ωc
求截止频率ωc