(1)E(Y)=0×0.001+1×0.010+2×0.060+3×0.185+4×0.324+5×0.302+6×0.118=4.2
(2)σ2=02×0.001+12×0.010+22×0.060+32×0.185+42×0.324+52×0.302+62×0.118–4.22=1.257
(简答题)
Y为垂钓者在一小时内钓上的鱼数,其概率分布如下表:问: (1)期望一小时内钓到的鱼数? (2)它们的方差? 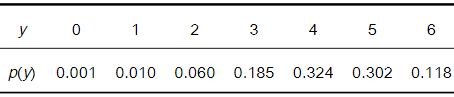
正确答案
答案解析
略
相似试题
(简答题)
设X和Y分别表示两个不同电子器件的寿命(以小时计),并设X和Y相互独立,且服从同一分布,其概率密度为 求Z=X/Y的概率密度.
(简答题)
某种电子元件的寿命X是随机变量,其概率密度为 求(1)常数C; (2)若将3个这种元件串联在一条线路上,试计算该线路使用150小时后仍能正常工作的概率。
(填空题)
设随机变量X和Y相互独立,其概率分布分别为,则P{X=Y}=()
(单选题)
设随机变量X与Y相互独立,其概率分布分别为 则有()
(简答题)
设X,Y是相互独立的随机变量,其概率密度分别为 求E(XY).
(单选题)
设二维随机变量(X,Y)服从区域D://x2+y2≤1上的均匀分布,则(X,Y)的概率密度为()
(简答题)
某学校在一次考试后,从考生中按简单随机抽样方式抽取90名学生,对语文课程的考试成绩进行检查,得知其平均分数为62.5分,样本标准差为7.45分。要求: 1.以95.45%的概率保证程度推断全部考生语文考试成绩的区间范围; 2.如果其他条件不变,将允许误差缩小一半,应抽取多少名学生?
(简答题)
已知随机变量X服从[0,2]上的均匀分布,求Y=3X-1的概率密度函数.
(简答题)
设随机变量X服从(0,1)上的均匀分布,求Y=eX的概率密度函数.



