(单选题)
以双曲线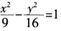 的右焦点为圆心,且与其渐近线相切的圆方程是()。
的右焦点为圆心,且与其渐近线相切的圆方程是()。
Ax2+y2-10x+9=0
Bx2+y2-10x+16=0
Cx2+y2+10x+16=0
Dx2+y2+10x+9=0
正确答案
答案解析
略
相似试题
(简答题)
一圆与y轴相切,圆心在x-3y=0上,在y=x上截得的弦长为,求圆的方程。
(简答题)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1。 (1)求椭圆C的标准方程; (2)若直线Z:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证:直线l过定点,并求出该定点的坐标。
(简答题)
已知椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点D,从每条曲线上取两个点,将其坐标记录于下表中: (1)求C1、C2的标准方程: (2)请问是否存在直线L满足条件:①过C2的焦点F;②与C1交不同两点M、N,且满足若存在,求出直线L的方程;若不存在,说明理由。
(单选题)
篮球三分投篮区是以篮圈中心点的投影为圆心,距离端线中点的内沿()处,以6.25米为半径的圆形。
(单选题)
半圆形闸门半径为R,将其垂直放入水中,且直径与水面齐,设水密度ρ=1。若坐标原点取在圆心,x轴正向朝下,则闸门所受压力p为()。
(单选题)
抛物线y2=4x的焦点为F,准线为l,经过F且斜率为的直线与抛物线在x轴上方的部分相交于点A,AK⊥l,垂足为K,则△AKF的面积是()。
(单选题)
如图,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心c的轴线上有a、b、d三个点,a和b、b和c、c和d间的距离均为R,在a点处有一电荷量为q(q>O)的固定点电荷,已知b点处的场强为零,则d点处场强的大小为()(k为静电力常量)
(单选题)
下图为北京时间上午7点时的光照图,弧AB为晨昏线与70°纬线相切,读图回答问题。 此时()。
(单选题)
将植物横放,测量根和茎生长素浓度与其生长状况的关系如甲图所示,则曲线上M、N、P和Q点分别最可能对应于乙图中的()。


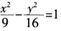 的右焦点为圆心,且与其渐近线相切的圆方程是()。
的右焦点为圆心,且与其渐近线相切的圆方程是()。 