的直线与抛物线在x轴上方的部分相交于点A，AK⊥l，垂足为K，则△AKF的面积是（）。 
（单选题）
抛物线y2=4x的焦点为F，准线为l，经过F且斜率为
的直线与抛物线在x轴上方的部分相交于点A，AK⊥l，垂足为K，则△AKF的面积是（）。
A4
B3
C4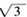
D8
正确答案
答案解析
略
相似试题
（单选题）
已知AB为过抛物线y2=2px焦点F的弦，则以AB为直径的圆与抛物线的准线（）。
（单选题）
设坐标原点为O，抛物线y2：2x与过焦点的直线交于A、B两点，则（）。
（简答题）
已知椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点D，从每条曲线上取两个点，将其坐标记录于下表中： （1）求C1、C2的标准方程： （2）请问是否存在直线L满足条件：①过C2的焦点F；②与C1交不同两点M、N，且满足若存在，求出直线L的方程；若不存在，说明理由。
（简答题）
已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1。 （1）求椭圆C的标准方程； （2）若直线Z：y=kx+m与椭圆C相交于A，B两点（A，B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点。求证：直线l过定点，并求出该定点的坐标。
（简答题）
已知定点P（6，4）与定直线l1：y=4x，过P点的直线l与l1交于第一象限Q点，与x轴正半轴交于点M，求使△OQM面积最小的直线l方程。
（填空题）
（）和（）根据教师的需要和不同时期所关注的焦点问题，将教师的成长划分为三个发展阶段。
（单选题）
以双曲线的右焦点为圆心，且与其渐近线相切的圆方程是（）。
（单选题）
（）依据教师的需要和不同时期所关注的焦点问题，将教师的成长划分为关注生存、关注情境和关注学生三个阶段。
（简答题）
已知曲线x2+2y2+4x+4y+4=0按向量a=（2，1）平移后得到曲线C。 （1）求曲线C的方程； （2）过点D（0，2）的直线l与曲线C相交于不同的两点M、N，且M在D、N之间，设，求实数λ的取值范围。
