
(简答题)
已知能带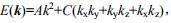 (1)在k空间中有效质量倒数矩阵,并将其对角化, (2)并找出主轴方向。
(1)在k空间中有效质量倒数矩阵,并将其对角化, (2)并找出主轴方向。
正确答案
如下:


答案解析
略
相似试题
(简答题)
已知在紧束缚近似下,体心立方晶体s态电子构成的能带为: (1)求能带宽度, (2)求电子在能带中的运动速度,求带底和带顶的速度, (3)求电子的有效质量倒数张量,求带底和带顶的有效质量。
(简答题)
已知在紧束缚近似下,面心立方晶体s态电子构成的能带为: (1)求能带宽度。 (2)求带低的有效质量。 (3)证明,在布里渊区中心,等能面近似为球形。并求布里渊区中心附近的有效质量。
(简答题)
已知晶格常数为a的简单立方晶系,s态电子构成的能带为,测得带顶的有效质量为,求: (1)参数B, (2)求能带宽度, (3)布里渊区中心附近电子的态密度。
(简答题)
已知硅的导带及其价带的有效态密度Nn,Np在室温(300K)时分别为2.8×1019cm-3,1.15×1019cm-3。试计算电子的有效质量mn及空穴的有效质量mp。已知h=6.63×10-34Js,kB=1.38×10-23J/K。
(简答题)
已知质量为m的质点处于某力场中位置矢量为r的地方,其势能可以表示为,其中k为常量。 (1)画出势能曲线; (2)求质点所受力的形式; (3)证明此力是保守力。
(简答题)
用紧束缚模型求最近邻近似的s态电子能带公式,写出二维正三角形网络的能带,计算电子的速度及有效质量张量。
(简答题)
金属铋的导带底部有效质量倒数张量为
(简答题)
用紧束缚近似求出面心立方金属和体心立方金属中与s态原子能级对应的能带的E(k)函数。
(填空题)
已知lmol的某种理想气体(其分子可视为刚性分子),在等压过程中温度上升1K,内能增加了20.78J,则气体对外作功为()气体吸收热量为()。(普适气体常量R=8.31.J•mol-1•K-1)


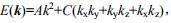 (1)在k空间中有效质量倒数矩阵,并将其对角化, (2)并找出主轴方向。
(1)在k空间中有效质量倒数矩阵,并将其对角化, (2)并找出主轴方向。 