
(简答题)
已知某种机械零件的直径X(mm)服从正态分布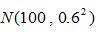 规定直径在100±1.2(mm)之间为合格品,求这种机械零件的不合格品率。
规定直径在100±1.2(mm)之间为合格品,求这种机械零件的不合格品率。
正确答案

答案解析
略
相似试题
(简答题)
测得16个零件的长度(mm)如下: 设零件长度服从正态分布,求零件长度标准差的置信水平为0.99的置信区间.如果: (1)已知总体均值为12.08mm; (2)未知总体均值。
(简答题)
一台自动机床加工零件的直径服从正态分布,加工要求为E(X)=5cm。现从一天的产品中抽取50个,分别测量直径后算得,标准差0.6cm。试在显著性水平0.05的要求下检验这天的产品直径平均值是否处在控制状态(用临界值规则)?
(简答题)
从某同类零件中抽取9件,测得其长度为(单位:mm): 6.0;5.7;5.8;6.5;7.0;6.3;5.6;6.1;5.0 设零件长度X服从正态分布N(μ,1)。求μ的置信度为0.95的置信区间。
(简答题)
工厂生产一种零件,其口径X(单位:毫米)服从正态分布N(μ,σ2),现从某日生产的零件中随机抽出9个,分别测得其口径如下: 14.6;14.7;15.1;14.9;14.8;15.0;15.1;15.2;14.7 已知零件口径X的标准差σ=0.15,求μ的置信度为0.95的置信区间。
(简答题)
一工厂生产的某种元件的寿命X(以小时计)服从均值μ=160,均方差为σ的正态分布,若要求允许最大为多少?
(简答题)
自动车床加工某种零件,零件的长度服从正态分布。现在加工过程中抽取16件,测得长度值(单位:毫米)为: 试对该车床加工该种零件长度值的数学期望进行区间估计(置信概率0.95)。
(简答题)
已知猪血红蛋白含量x服从正态分布N(12.86,4),若P(x<I1)=0.03,P(x≥I2)=0.03,求1I,I2。
(简答题)
据一个汽车制造厂家称,某种新型小汽车耗用每加仑汽油至少能行驶25公里,一个消费者研究小组对此感兴趣并进行检验。检验时的前提条件是已知生产此种小汽车的单位燃料行驶里程技术性能指标服从正态分布,总体方差为4。试回答下列问题:
(简答题)
据一个汽车制造厂家称,某种新型小汽车耗用每加仑汽油至少能行驶25公里,一个消费者研究小组对此感兴趣并进行检验。检验时的前提条件是已知生产此种小汽车的单位燃料行驶里程技术性能指标服从正态分布,总体方差为4。试回答下列问题:


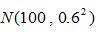 规定直径在100±1.2(mm)之间为合格品,求这种机械零件的不合格品率。
规定直径在100±1.2(mm)之间为合格品,求这种机械零件的不合格品率。 