（题干）
本题共计 5 个问题
已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。
简答题
第 1 题
从直观及经济角度解释α和β。
正确答案
α+βN为接受过N年教育的员工的总体平均起始薪金。当N为零时，平均薪金为α，因此α表示没有接受过教育员工的平均起始薪金。β是N每变化一个单位所引起的E的变化，即表示每多接受一年教育所对应的薪金增加值。
答案解析
略
简答题
第 2 题
OLS估计量
和
满足线性性、无偏性及有效性吗？简单陈述理由。
和
满足线性性、无偏性及有效性吗？简单陈述理由。 正确答案
OLS估计量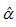
和
仍满足线性性、无偏性及有效性，因为这些性质的的成立无需随机扰动项的正态分布假设。
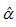和
仍满足线性性、无偏性及有效性，因为这些性质的的成立无需随机扰动项的正态分布假设。 答案解析
略
简答题
第 3 题
对参数的假设检验还能进行吗？简单陈述理由。
正确答案
如果μt的分布未知，则所有的假设检验都是无效的。因为t检验与F检验是建立在μ的正态分布假设之上的。
答案解析
略
简答题
第 4 题
如果被解释变量新员工起始薪金的计量单位由元改为100元，估计的截距项、斜率项有无变化？
正确答案
考察被解释变量度量单位变化的情形。以E*表示以百元为度量单位的薪金，则
E.E*×100=α+βN+μ
由此有如下新模型
E.=（α/100）+（β/100）N+（μ/100）
或E*=α*+β*N+μ*
这里α*=α/100，β*=β/100。所以新的回归系数将为原始模型回归系数的1/100。
E.E*×100=α+βN+μ
由此有如下新模型
E.=（α/100）+（β/100）N+（μ/100）
或E*=α*+β*N+μ*
这里α*=α/100，β*=β/100。所以新的回归系数将为原始模型回归系数的1/100。
答案解析
略
简答题
第 5 题
若解释变量所受教育水平的度量单位由年改为月，估计的截距项与斜率项有无变化？
正确答案
再考虑解释变量度量单位变化的情形。设N*为用月份表示的新员工受教育的时间长度，则N*=12N，于是
E=α+βN+μ=α+β（N*/12）+μ
或E=α+（β/12）N*+μ
可见，估计的截距项不变，而斜率项将为原回归系数的1/12。
E=α+βN+μ=α+β（N*/12）+μ
或E=α+（β/12）N*+μ
可见，估计的截距项不变，而斜率项将为原回归系数的1/12。
答案解析
略
相似试题
（简答题）
已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。对参数的假设检验还能进行吗？简单陈述理由。
（简答题）
已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。如果被解释变量新员工起始薪金的计量单位由元改为100元，估计的截距项、斜率项有无变化？
（简答题）
已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。若解释变量所受教育水平的度量单位由年改为月，估计的截距项与斜率项有无变化？
（单选题）
一元线性回归模型Yi=β0+β1Xi+μi的最小二乘回归结果显示，残差平方和RSS=40.32，样本容量n=25，则回归模型的标准差σ为（）。
