
求两个平行平面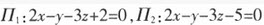 之间的距离。
之间的距离。
正确答案

答案解析
相似试题
(单选题)
两个带等量异号电荷的无限大平行平面之间的电场场强E为()
(简答题)
求经过点A(-1,2,3),垂直于直线,且与平面Ⅱ:7x+8y+9z+10=0平行的直线方程。
(单选题)
底面为平行四边形的四棱柱与平行六面体这两个概念的外延之间具有()关系。
(简答题)
Rt△ABC中,∠C=90°,BC=36,若平面ABC外一点P与平面A,B,C三点等距离,且P到平面ABC的距离PH为80,M为AC的中点。 (1)求证:PM⊥AC; (2)求P到直线AC的距离; (3)求PM与平面ABC所成角的正切值。
(简答题)
已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点。 (1)求证:平面EBD⊥平面ABCD; (2)求点E到平面PBC的距离; (3)求二面角A-BE-D的大小。
(简答题)
针对“点到直线的距离公式”,有两位老师分别设计了以下两个教学片段。请你分析哪一个教学情境更好。 (一)师:一条河的两岸可以看成平行的直线,某人在岸边要驾驶船到对岸,请问,他应该选择在哪个位置到对岸,才能以最短的路径实现目的? 生:随便那个位置都可以,因为岸的一边上任意点到对岸的距离都相等。 师:为什么? 生:感觉。 师:这种感觉很好,但我们应该给予证明。今天,我们就来学习点到直线的距离公式。 …… (二)师:前面我们学习了平面上两直线的位置关系:平行与相交。当两直线相交时,我们采用角来刻画它们的“相交程度”。那么,如果两直线平行时,我们采用什么方法来刻画呢?(师平行地拿两支笔进行远近移动) 生:距离。 师:什么意思? 生:你刚才在比划,给我们一个感觉,两平行直线有远和近的区别。 师:好,那么怎样刻画两直线的距离呢? 生甲:作任意一条直线与两直线都垂直,被它们所截得的线段长度都相等,这个长度我们就定义为两平行线的距离。 师:很好!但要说明怎么作任意直线与两直线都垂直,还有别的什么方法? 生乙:其实,两平行直线上的一点到另一条直线的距离相等,这个距离可以定义为两平行直线间的距离。 师:很好!为了研究两平行直线的距离,我们可以选择甲和乙的办法,大家看,该选择哪个办法? 生丙:选择甲,因为点到点的距离最原始。 生丁:选择乙,因为点到直线的距离也是通过点到点的距离来刻画的,如果能够得到点到直线的距离,可以少走弯路。 师:两位同学的构思都有道理,那么,我们就合二为一。今天,我们就开始学习点到直线的距离。 ……
(单选题)
在一个采用粗缆作为传输介质的以太网中,两个节点之间的距离超过500m,那么最简单的方法是选用()来扩大局域网覆盖范围。
(单选题)
伽利略通过梁的弯曲试验和理论分析,指出对长度相似的圆柱形梁,抗弯力矩和半径立方成比例;1685年,牛顿发现了万有引力定律:两个物体之间有引力,引力和距离的平方成反比,和两个物体质量的乘积成正比。从这两个事例中可以看出自然科学的特征之一是()
(简答题)
求与直线及直线都平行且经过坐标原点的平面方程。


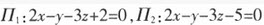 之间的距离。
之间的距离。 