质量为10×10-3kg的小球与轻弹簧组成的系统,按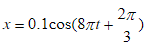 的规律作振动,式中t以秒(s)计,x以米(m)计.求: (1)振动的圆频率、周期、振幅、初位相; (2)振动的速度、加速度的最大值; (3)最大回复力、振动能量、平均动能和平均势能。
的规律作振动,式中t以秒(s)计,x以米(m)计.求: (1)振动的圆频率、周期、振幅、初位相; (2)振动的速度、加速度的最大值; (3)最大回复力、振动能量、平均动能和平均势能。
正确答案
可知圆频率为:ω=8π,周期T=2π/ω=1/4=0.25(s),振幅A=0.1(m),初位相θ=2π/3.
(2)速度的最大值为:vm=ωA=0.8π=2.51(m∙s-1);
加速度的最大值为:am=ω2A=6.4π2=63.2(m·s-2).
(3)弹簧的倔强系数为:k=mω2,最大回复力为:f=kA=mω2A=0.632(N);
振动能量为:E=kA2/2=mω2A2/2=3.16×10-2(J),
平均动能和平均势能为:kpEE=kA2/4=mω2A2/4=1.58×10-2(J).
答案解析
相似试题
(简答题)
质量为m=10X10-3kg的小球与轻弹簧组成的系统,按的规律作简谐振动,式中t以秒为单位,x以米为单位。试求: (1)振动的圆频率、周期、振幅、初位相以及速度和加速度的最大值; (2)求t=1s,2s,10s时刻的位相。 (3)利用Mathematica绘出位移、速度、加速度与时间的关系曲线。
(填空题)
一质量为40×10-3kg的子弹,以1000m/s的速度飞行,它的德布罗意波长为(),所以子弹不显示()。
(简答题)
中和10-3kg聚酯用去浓度为10-3mol/L的NaOH0.012L,如果聚酯是由ω-羟基羧酸制得,计算它的数均相对分子质量。
(简答题)
如图所示,把质量m=0.20kg的小球放在位置A时,弹簧被压缩Δl=7.5×10-2m.然后在弹簧弹性力的作用下,小球从位置A由静止被释放,小球沿轨道ABCD运动.小球与轨道间的摩擦不计.已知BCD是半径r=0.15m的半圆弧,AB相距为2r.求弹簧劲度系数的最小值.
(简答题)
如图所示,把质量m=0.20kg的小球放在位置A时,弹簧被压缩Δl=7.5×10-2m.然后在弹簧弹性力的作用下,小球从位置A由静止被释放,小球沿轨道ABCD运动.小球与轨道间的摩擦不计.已知BCD是半径r=0.15m的半圆弧,AB相距为2r.求弹簧劲度系数的最小值.
(简答题)
质量为2.8×10-3kg、温度为300K、压强为标准大气压的氮气,等压膨胀到原来体积的两倍。求氮气所作的功Wp、吸收的热量Qp以及内能的增量ΔU。
(简答题)
与轻弹簧的一端相接的小球沿x轴作简谐振动,振幅为A,位移与时间的关系可以用余弦函数表示。若在t=0时,小球的运动状态分别为: (1)x=-A; (2)过平衡位置,向x轴正方向运动; (3)过x=A/2处,向x轴负方向运动; (4)过x=A/处,向x轴正方向运动。 试确定上述各状态的初相位。
(简答题)
一质量M=10kg的物体放在光滑的水平桌面上,并与一水平轻弹簧相连,弹簧的倔强系数K=1000N/m。今有一质量m=1kg的小球以水平速度v0=4m/s飞来,与物体M相撞后以v1=2m/s的速度弹回,试问: (1)弹簧被压缩的长度为多少?小球和物体的碰撞是完全弹性碰撞吗? (2)若小球和物体相撞后粘在一起,则上面所问的结果又如何?
(简答题)
一质量为10×10-3kg的物体作谐振动,振幅为24cm,周期为4.0s,当t=0时位移为+24cm (1)t=0.5时,物体所在的位置及此时所受力的大小和方向; (2)由起始位置运动到x=12cm处所需的最短时间; (3)在x=12cm处物体的总能量.


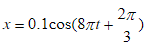 的规律作振动,式中t以秒(s)计,x以米(m)计.求: (1)振动的圆频率、周期、振幅、初位相; (2)振动的速度、加速度的最大值; (3)最大回复力、振动能量、平均动能和平均势能。
的规律作振动,式中t以秒(s)计,x以米(m)计.求: (1)振动的圆频率、周期、振幅、初位相; (2)振动的速度、加速度的最大值; (3)最大回复力、振动能量、平均动能和平均势能。 